Formation of Stationary Waves on String

In a sonometer wire the tension is maintained by suspending a 50.7 kg mass from the free end of the wire. The suspended mass has volume of 0.0075m^​3. The fundamental frequency of the wire is 260Hz. Find the new fundamental frequency if the suspended mass is completely submerged in water

The fundamental frequencies of two copper wire of same length are in the ratio $1:2$. If the tension on the wires are$729 \mathrm{g}$ and $324 \mathrm{g}$ respectively, then the ratio of their diameters will be:

A string of length $1 \mathrm{m}$ and mass $2\times {10}^{-5} \mathrm{kg}$ is under tension $T$. When the string vibrates, two successive harmonics are found to occur at frequencies $750 \mathrm{Hz}$ and $1000 \mathrm{Hz}$. The value of tension $T$ is _____ newton.

A wire of density $8\times {10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$ is stretched between two clamps $0.5 \mathrm{m}$ apart. The extension developed in the wire is $3.2\times {10}^{-4} \mathrm{m}$. If $Y=8\times {10}^{10} \mathrm{N} {\mathrm{m}}^{-2}$, the fundamental frequency of vibration in the wire will be _____ $\mathrm{Hz}$

A guitar string of length $90 \mathrm{cm}$ vibrates with a fundamental frequency of $120 \mathrm{Hz}$. The length of the string producing a fundamental of $180 \mathrm{Hz}$ will be _____ $\mathrm{cm}$

In an experiment with sonometer when a mass of $180 \mathrm{g}$ is attached to the string, it vibrates with fundamental frequency of $30 \mathrm{Hz}$. When a mass $m$ is attached, the string vibrates with fundamental frequency of $50 \mathrm{Hz}$. The value of $m$ is ______ $\mathrm{g}$.

The fundamental frequency of vibration of a string between two rigid support is $50 \mathrm{Hz}$. The mass of the string is $18 \mathrm{g}$ and its linear mass density is $20 \mathrm{g} {\mathrm{m}}^{-1}$. The speed of the transverse waves so produced in the string is _______ $\mathrm{m} {\mathrm{s}}^{–1}$.

A standing wave $y=A\sin \left(\frac{20\pi x}{3}\right) \cos \left(1000\pi x\right)$is maintained in a taut string where $y$ and $x$ are expressed in meters. The distance between the successive points oscillating with the amplitude$\frac{A}{2}$ across a node is equal to

A $100 \mathrm{cm}$ string fixed at both ends produces successive resonance frequency $384 \mathrm{Hz}$ and $288 \mathrm{Hz}$. Wave speed in string is $24n$ $\mathrm{m} {\mathrm{s}}^{-1}$. Find the value of$n$.

When a tuning fork vibrates with $1.0 \mathrm{m}$ or $1.05 \mathrm{m}$ long wire (both in same mode), $5$ beats per second are produced in each case. If the frequency of the tuning fork is $5f$ (in $Hz$) find$f$.

A $100 \mathrm{cm}$ string fixed at both ends produces successive resonance frequency $384 \mathrm{Hz}$ and $288 \mathrm{Hz}$. Wave speed in string is $16P \mathrm{m} {\mathrm{s}}^{-1}$, then$P$ is

Equation of a stationary wave can be expressed as $y=8\sin \frac{\pi x}{4} \cos 20\pi t$ here$x$and $y$ are in cm and$t$ in second, wavelength of any component of  progressive wave is

Write down an expression for the fundamental frequency of transverse vibration of a stretched string. If the vibrating wire is touched lightly at a point $\frac{1}{3}$rd distance from one end, what will happen?

A string vibrates with a frequency of $210 \mathrm{Hz}$. Another frequency with which the string can vibrate is $300 \mathrm{Hz}$. The number of harmonic of the first frequency is

A steel wire $8\times {10}^{-4} \mathrm{m}$ in diameter is fixed to a support at one end and is wrapped round a cylindrical tuning peg $5 \mathrm{mm}$ in diameter at the other end. The length of the wire between the peg and the support is $0.06 \mathrm{m}$. The wire is initially kept taut but without any tension. If the fundamental frequency of vibration of the wire if it is tightened by giving the peg a quarter of a turn is $1.08\times {10}^{\mathrm{n}}\mathrm{Hz}$. Then find the value of $n$
Density of steel $=7800 \mathrm{kg}/{\mathrm{m}}^3,Y$ of steel $=20\times {10}^{10} {\mathrm{Nm}}^{-2}$.

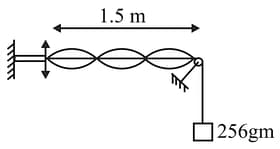
A string is stretched between a pulley and a wave generator consisting of a plate vibrating up and down with small amplitude and frequency $120 \mathrm{Hz}$. The standing wave pattern has $4$ nodes as shown. What should be the load (in gm) we want a standing wave with $5$ nodes.

A string will break apart if it is placed under too much tensile stress. One type of steel has density. ${\rho }_{\mathrm{steel} }={10}^4 \mathrm{kg} {\mathrm{m}}^{-3}$ and breaking stress $\alpha =9\times {10}^8 \mathrm{N} {\mathrm{m}}^{-2}$. We make a guitar string from $\left(4\pi \right)$ gram of this type of steel. It should be able to withstand $\left(900\pi \right)N$ without breaking. What is highest possible fundamental frequency (in $\mathrm{Hz}$ ) of standing waves on the string if the entire length of the string vibrates?

Choose correct statements

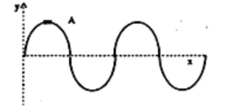
The distance between two successive nodes is .

A spring, fixed at one end, is connected to a steel wire of length $L$. The other end of the steel wire is connected to an AC source providing a sinusoidal signal of fixed frequency $f$. This stretches the spring and produces standing waves. The spring stretched by $18 \mathrm{cm}$ produces a standing wave with four antinodes in the steel wire. The stretch of the spring which will produce a standing wave of three antinodes is